Skl Un Fisika : Gerak

SKL UN Fisika : Gerak

Indikator 2.1
Menentukan besaran-besaran fisis gerak lurus, gerak melingkar beraturan, atau gerak parabola.

Materi

GERAK LURUS
Terkait dengan besaran pada gerak lurus, ada enam besaran yang tiga di antaranya merupakan besaran skalar dan tiganya lagi besaran vektor.
Besaran skalar :
Jarak dalam s
Kelajuan dalam v=Δs/Δt
Perlajuan dalam a = Δv/Δt
Besaran vektor :
Perpindahan dalam s
Kecepatan dalam v=Δs/Δt
Percepatan dalam a = Δv/Δt

Gerak Lurus Beraturan (GLB)
Pada gerak lurus beraturan, berlaku a = 0.

Grafik Gerak Lurus Beraturan (GLB)

Pada GLBB berlaku :
v = v₀ + a t
s = v₀ t + ½ a t²
v=v₀² + 2 a s
Grafik Gerak Lurus Berubah Beraturan (GLBB)




GERAK MELINGKAR BERATURAN
Gerak melingkar beraturan yaitu gerak suatu benda yang lintasannya berupa bulat dengan kelajuan tetap. Besaran-besaran pada gerak melingkar beraturan, mencakup periode (T), frekuensi (f), kelajuan linier (v), kecepatan sudut (w), percepatan sentripetal (a_s) dan gaya sentripetal (F)
Periode dan frekuensi :

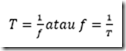
Kelajuan linier :

Kecepatan sudut

Hubungan antara kelajuan linier dan kecepatan sudut
v = ωr
Percepatan sentripetal :

Gaya sentripetal :
F_s = m a_s

GERAK PARABOLA
Gerak parabola merupakan gerak benda yang melaksanakan gerak lurus beraturan dan gerak lurus beraturan secara serentak. Dalam menganalisa gerak parabola ini, kita melihatnya sebagai gerak yang terpisah antara gerak lurus beraturan (GLB) pada sumbu-x dan gerak lurus berubah beraturan (GLBB) pada sumbu-y.

Besaran	Sumbu-X	Sumbu-Y
	Gerak lurus beraturan	Gerak lurus berubah beraturan
Kecepatan awal	v0x = v0 cos α	v0y = v0 sin α
Perpindahan	x	y
Waktu	t	t
Percepatan	ax=0	ay=-g
Kecepatan akhir	vtx = v0x	vty = v0y + ay t vty = v0y – gt
Perpindahan	x= v0x t	y = v0y t + ½ ay t2 y = v0y t – ½ gt2

Untuk soal-soalnya menyusul ya? Pada postingan berikutnya.
Sumber https://arsyadriyadi.blogspot.com/